ICCV 2013 |
||
Curvature-aware Regularization |
| Kwang In Kim | James Tompkin | Christian Theobalt |
| MPI for Informatics | Intel Visual Computing Institute |
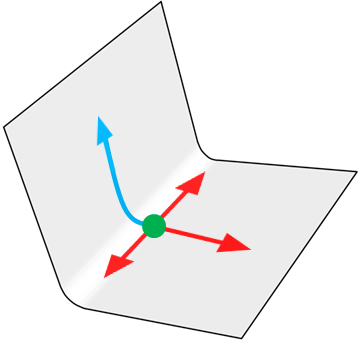 |
A manifold with high extrinsic curvature and zero intrinsic curvature
at the green dot. Since it has zero intrinsic curvature here, intrinsically it is equivalent to
R2. |
| Abstract | |
One fundamental assumption in object recognition as well as in other computer vision and pattern recognition problems is that the data generation process lies on a manifold and that it respects the intrinsic geometry of the manifold. This assumption is held in several successful algorithms for diffusion and regularization, in particular, in graph-Laplacian-based algorithms. We claim that the performance of existing algorithms can be improved if we additionally account for how the manifold is embedded within the ambient space, i.e., if we consider the extrinsic geometry of the manifold. We present a procedure for characterizing the extrinsic (as well as intrinsic) curvature of a manifold M which is described by a sampled point cloud in a high-dimensional Euclidean space. Once estimated, we use this characterization in building anisotropic diffusion and regularization on M (Fig. 1, below), and form a new regularizer on a point cloud. The resulting re-weighted graph Laplacian demonstrates superior performance over classical graph Laplacian in semi-supervised learning and spectral clustering.
|
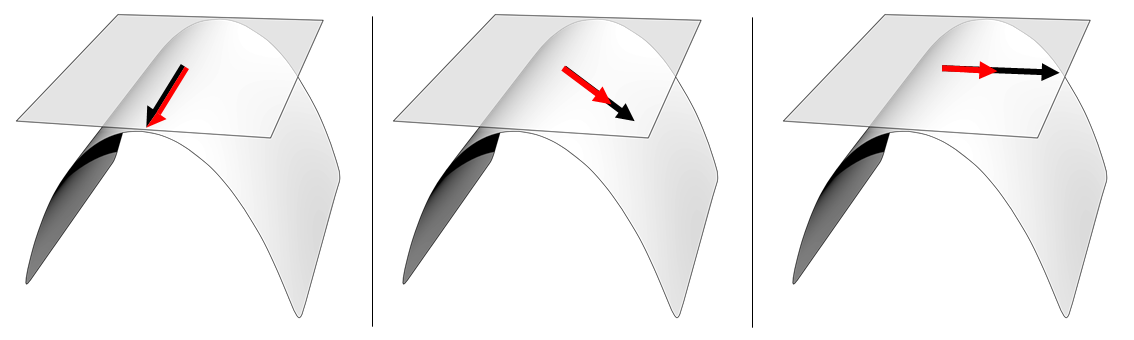 |
Figure 1: Examples of applying our diffusivity operator Dp to vectors in Tp(M): Evaluation point p is at the origin of each vector arrow. A two-dimensional surface manifold M embedded in R3 is generated by bending a plane along a fixed direction. The tangent space Tp(M) is shown as a transparent plane. (Left) When the black input vector is orthogonal to the bending direction along which M has no curvature, the resulting red output vector is identical to the input; (Right) If the input is parallel to the bending direction along which M is maximally curved, the output is maximally shrunken. In particular, when the curvature is infinite, the output vector is zero. (Middle) In general, the input vector is shrunk depending on how M is curved along the direction of input.
|
|
@article{KimTomThe13,
|
| Resources | ||
|


