Quantum Permutation Synchronization

Tolga Birdal1, *     Vladislav Golyanik2, *     Christian Theobalt2     Leonidas Guibas1
1Stanford University      2Max Planck Institute for Informatics, Saarland Informatics Campus
* both authors contributed equally
CVPR, 2021

Overview of QuantumSync. The input to our method is a set of correspondences (permutations) either between two 2D images or two 3D shapes (top-left). In the first step, we formulate permutation synchronization in the form consumable by modern adiabatic quantum computers (AQC) such as D-Wave Advantage system 1.1, i.e., as a quadratic unconstrained binary optimization (QUBO) problem. The visualization of the matrix of weights Q from an exemplary QUBO is shown on top in the middle. Q is a real symmetric matrix, with non-zero elements highlighted in blue. The obtained QUBO is a logical problem, which can be visualized as a graph in which each node corresponds to a qubit, and each edge denotes an interaction between two qubits (top-right). To execute QuantumSync, we further perform minor embeddeding, i.e., a mapping of the obtained logical problem to the quantum hardware topology (Pegasus graph). This mapping requires multiple physical qubits to represent a single logical qubit, due to the characteristics of modern AQC processors. On the bottom-right, we show an excerpt of the minor-embedded problem, with yellow colour highlighting a chain of physical qubits representing one logical qubit. Next, the QUBO is solved on AQC by running multiple quantum annealings (the histogram of the resulting energies is shown on the bottom in the middle) and selecting the solution with the lowest energy among all runs for unembedding, i.e., interpretation of the measured bitstring as a solution to the target problem (permutation synchronization). See the paper for more details.

Abstract

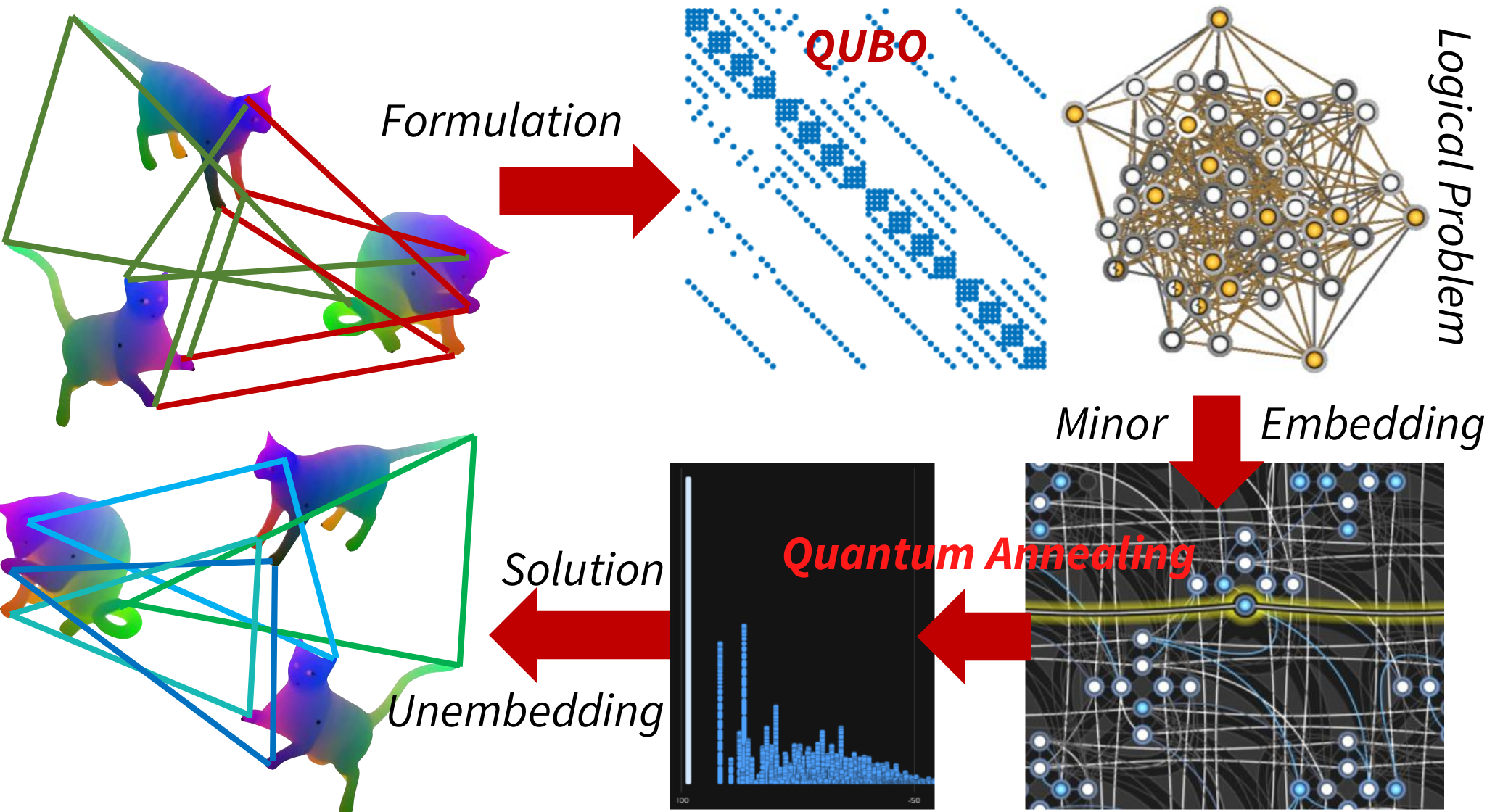
We present QuantumSync, the first quantum algorithm for solving a synchronization problem in the context of computer vision. In particular, we focus on permutation synchronization which involves solving a non-convex optimization problem in discrete variables. We start by formulating synchronization into a quadratic unconstrained binary optimization problem (QUBO). While such formulation respects the binary nature of the problem, ensuring that the result is a set of permutations requires extra care. Hence, we: (i) show how to insert permutation constraints into a QUBO problem and (ii) solve the constrained QUBO problem on the current generation of the adiabatic quantum computers D-Wave. Thanks to the quantum annealing, we guarantee global optimality with high probability while sampling the energy landscape to yield confidence estimates. Our proof-of-concepts realization on the adiabatic D-Wave computer demonstrates that quantum machines offer a promising way to solve the prevalent yet difficult synchronization problems.

Overview

Context and Goals: Many computer vision problems can be interpreted as synchromization problems over permutations. Synchronization simultaneously averages the pairwise local information into a global one. This procedure is a fundamental piece of most state-of-the-art multi-view reconstruction and multi-shape analysis pipelines. In this paper, our focus is permutation synchronization, where the edges of the graph are labeled by permutation matrices denoting the correspondences either between two 2D images or two 3D shapes. Specifically, we seek to find an absolute ordering for each point of each frame which sorts all the corresponding points into the same bin. Unfortunately, this problem by definition involves a combinatorial non-convex optimization, for which attaining the global minimum is intractable under standard formulations targeting classical von Neumann computers. Because on a classical computer we cannot speak of a global optimality guarantee of our discrete problem, we turn our attention to a new family of processors, i.e., quantum computers.

Quantum computers are computational machines which employ quantum effects of quantum superposition, entanglement and tunneling. The concept of quantum computers was proposed in the early '80s, and it has taken more than fifteen years until the first functional computers were demonstrated in laboratories. Nowadays, quantum computing hardware is mature so that real-world problems can benefit from it. In this paper, we focus on adiabatic quantum computers (AQC). The operational principle of AQC is grounded on the adiabatic theorem of quantum mechanics.

Contributions:

  1. Formulation of the classical synchronization in a form consumable by an AQC,
    i.e., quadratic unconstrained binary optimization (QUBO) problem.
  2. Introduction of permutations as linear constraints into the obtained QUBO problem.
  3. Numerical verification of our formulation in simulated experiments as well as on a real AQC
    (for the first time on D-Wave Advantage system 1.1).
  4. Extensive ablation studies giving insights into this new way of computing.

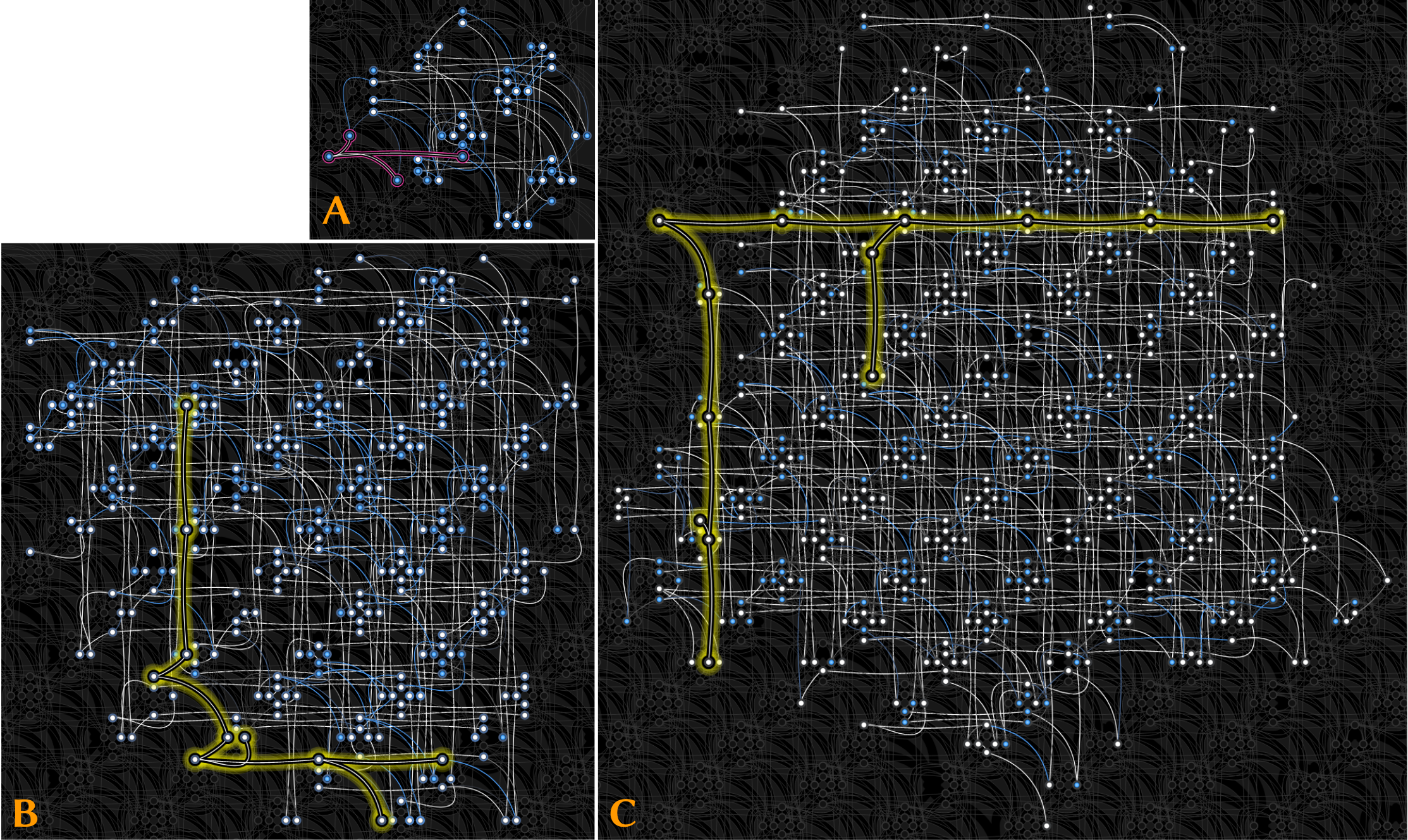
Minor Embeddings:

Exemplary minor embeddings in the experiments with three points and three views (A, 18 logical qubits, 49 physical qubits), four points and four views (B, 48 logical qubits, 341 physical qubits) and three points and eight views (C, 63 logical qubits, 550 physical qubits). In each case, we highlight qubit chains of the maximum chain length in the embedding, either in magenta (A, no warnings) or yellow (B and C, chain length warnings).

Summary: For small problem instances, QuantumSync achieves state-of-the-art accuracy in our experiments which is on par with classical best techniques (not considering exhaustive search). Experimenting on D-Wave Advantage system 1.1 (introduced in October 2020) allows us to minor-embed larger problems compared to the previous D-Wave AQC generation. The overall experimental QPU time in our experiments amounts to ≈15 minutes. All in all, we conclude that quantum computing hardware has reached the level that it can be applied to real-world computer vision and pattern recognition problems with high potential to improve upon the known classical methods.

Downloads




Related Works on Quantum Computer Vision

[project page]   A Quantum Computational Approach to Correspondence Problems on Point Sets (CVPR 2020)
[project page]   Adiabatic Quantum Graph Matching with Permutation Matrix Constraints (3DV 2020)
[project page]   Q-Match: Iterative Shape Matching via Quantum Annealing (arXiv, 2021)


Citation

BibTeX, 1 KB

@inproceedings{QuantumSync2021, 
       author = {{Birdal}, Tolga and {Golyanik}, Vladislav and {Theobalt}, Christian and {Guibas}, Leonidas}, 
        title = {Quantum Permutation Synchronization}, 
      booktitle = {Computer Vision and Pattern Recognition (CVPR)},
         year = {2021} 
}

Contact

For questions and clarifications please get in touch with:
Vladislav Golyanik golyanik@mpi-inf.mpg.de
This page is Zotero translator friendly. Page last updated Imprint. Data Protection.